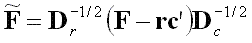 .
.CAR is an application for computing correspondence analysis that allows orthogonal and oblique rotations.
Two important features of CAR are:
(1) non-Matlab-users should be able to manage it.
(2) advanced users should find it useful. So the analysis should also be easily computed from Matlab command line.
Let F be an n × p contingency table divided by the total number of observations, 1i an i × 1 vector of ones, r = F1p, c = F'1n and Dr and Dc are diagonal matrices with the elements of r and c on the diagonal, respectively. By assigning weights to the rows and the columns of a matrix of deviations from independence, we obtain the following matrix of standardized residuals,
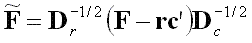 . . |
(1) |
The aim in correspondence analysis is to find k dimensional coordinate matrices X and Y, for row and column points, respectively, in such a way that the loss function
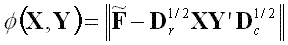 |
(2) |
is minimized subject to X'DrX = I and Y'DcY = I, where ||H||2 denotes the sum of squared elements of H. Let
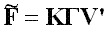 |
(3) |
be the singular value decomposition of matrix , where is a diagonal matrix with singular values on the diagonal, in weakly descending order, and K'K = V'V = I. As Van de Velden and Kiers (2005) pointed out, φ(X, Y) is minimized by
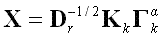 |
(4) |
and
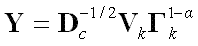 , , |
(5) |
where Kk and Vk are, respectively, the n × k and p × k matrices of singular vectors corresponding to the k largest singular values gathered in the k × k diagonal matrix Γk. Finally, α is the parameter that determines the type of coordinates in X and Y. Three choices are usually considered for α:
(a) α = 0: The column coordinates Y are referred to as principal coordinates and the row coordinates X as standard coordinates.
(b) α = 1: The column coordinates Y are referred to as standard coordinates and the row coordinates X as principal coordinates.
(c) α = .5: Both column and row coordinates are referred to as symmetrical coordinates.
An important feature of X and Y is that for any choice of α, the matrix product optimally approximates, in the sense that the sum of squared differences between and is as small as possible. Hence, these solutions can be interpreted as so-called biplots.
The distinction between principal, standard and symmetrical coordinates is fundamental in CA:
(a) Principal coordinates are the coordinates of the set of (column or row) variables that are studied. If α = 0, these coordinates are related to column variables, and if α = 1, to row variables.
(b) Standard coordinates are the coordinates of the set of (column or row) variables that help to describe the set of variables studied. If α = 0, these coordinates are related to row variables; and, if α = 1, to column variables.
(c) When symmetrical coordinates are chosen, both column and row coordinates are described.
The following models are allowed in CAR:
1. Symmetrical coordinates for rows and columns (Biplot model)
The rotations allowed in this situation are:
2. Principal coordinates for rows, and standard coordinates for columns
The rotations allowed in this situation are:
3. Principal coordinates for columns, and standard coordinates for rows
The rotations allowed in this situation are:
4. Principal coordinates for rows and columns (French symmetrical model)
No research has been done on the rotation of axes in this model, so rotations are not allowed with this model.
In the context of Exploratory Factor Analysis, loading matrices are frequently weighted before rotations are computed. After rotation, the original distances of points from the origin are reestablished, so the interpretation is not affected by the weights applied.
In the context of CA, other weighting schemes may also be applicable. Let Wx and Wy be diagonal matrices, with weights on the diagonal and zeros elsewhere. Wx and Wy are weighting matrices related to the coordinate matrices X and Y, respectively. The aim is to weight the rows of X and Y during the rotation, so that the products WxX and WyY are rotated (instead of X and Y). Three options for Wx and Wy can be considered:
(a)Each weighting matrix is defined as an identity matrix. With this option, no weight is actually applied.
(b)Due to the specific weighting in correspondence analysis, infrequently observed points are sometimes positioned relatively far away from the origin. In this situation, these particular points may play an important role in determining the rotation angle. To prevent this from happening, the coordinates can be rescaled using the corresponding masses (i.e. Wx = Dr-1/2 and Wy = Dc-1/2). This weighting procedure places infrequent points close to the origin, while others remain a long way from it.
(c) In the context of Exploratory Factor Analysis, it is common practice to carry out a row-wise normalization of the matrix to be rotated. In CA, this procedure involves rescaling the coordinates using and . With this scheme, all the rows have the same influence on the final position of the axes.